Esercizio 7 funzioni razionali intere

0

y=x^3-5x^2+7x-2

  • Insieme di definizione

Essendo una funzione razionale intera, il dominio è tutto \mathbb{R}.

  • Simmetrie e periodicità

-f(x)=-x^3+5x^2-7x+2

f(-x)=-x^3-5x^2-7x-2

Questa funzione non avrà simmetrie.

  • Intersezioni con gli assi

\begin{cases} x=0 \\ y=-2 \end{cases}

\begin{cases} y=0 \\ x=2 \quad x=\frac {3 \pm \sqrt 5}{2} \end{cases}

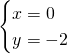
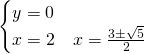
Per calcolare gli zeri di questa funzione, abbiamo utilizzato la regola di Ruffini sostituendo all’incognita il valore 2, e poi risolvendo l’equazione di secondo grado.

La funzione avrà quattro intersezioni con gli assi:

\left (0;-2 \right), \left (\frac {3 \pm \sqrt 5}{2};0 \right), e \left(2;0\right).

  • Segno della funzione

Studiamo la positività di f(x):

x^3-5x^2+7x-2 \geq0

\left(x-2 \right)\left (x-\frac {3 - \sqrt 5}{2} \right) \left(x-\frac {3 - \sqrt 5}{2} \right)\geq0

\frac {3 - \sqrt 5}{2} \leq x \leq 2 \quad \lor \quad x \geq \frac {3 + \sqrt 5}{2}

  • condizione agli estremi

    \[\lim_{ x \rightarrow \pm \infty} f(x)= \pm \infty\]

  • Asintoti

Essendo una funzione razionale intera non avrà asintoti verticali, orizzontali ne tantomeno obliqui.

  • Studio della derivata prima

y'=3x^2-10x+7

y' \geq 0

3x^2-10x+7 \geq0

(3x-7)(x-1) \geq0

x \leq 1 \quad \lor \quad x \geq \frac 73

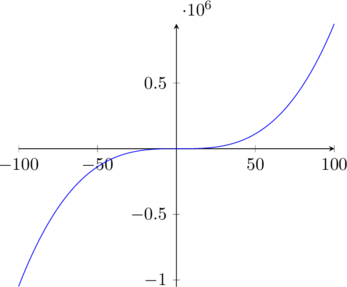
La funzione sarà crescente fino al punto (1;1), decrescente fino a \left( \frac 73;-\frac {5}{27}\right), e crescente fino a +\infty.

I punti trovati saranno proprio il massimo e il minimo relativo della funzione.

  • Studio della derivata seconda

y''=6x-10

y''\geq 0

6x-10 \geq0

x \geq \frac 53

La funzione avrà concavità verso il basso fino al punto di flesso F di ascissa \frac 53 e concavità verso l’alto in seguito.

 


Rendered by QuickLaTeX.com

 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 32 persone)

Lascia un commento