Cerchio e circonferenza

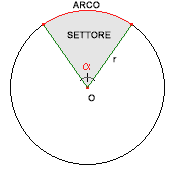
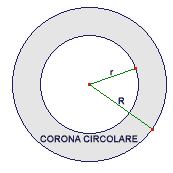
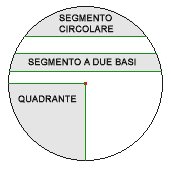
Lunghezza della circonferenza: $C=2\pi r$

Area del cerchio: $A=\pi r^2$

Lunghezza dell’arco: $l=\frac{C\alpha}{360}$ con $\alpha$ misurato in gradi

Area del settore circolare: $A=\frac{\pi r^2 \alpha}{360}$ ; $A=\frac 12 r^2 \alpha$

Area del semicerchio: $A=\frac 12 \pi r^2$

Area del quadrante: $A=\frac 14 \pi r^2$

Area della corona circolare:

$A=\pi (R^2-r^2)$

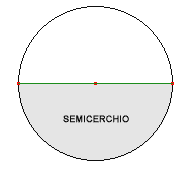
Area del segmento circolare: si trova come differenza fra l’area di un settore e l’area di un triangolo.

LEGENDA

Raggio = r

$semicerchio$	$settore$
$corona circolare$	$segmento circolare - segmento a due basi - quadrante$

» Teorema della corda:

$AB=2r sen \alpha$

$AB=2r sen (180-\alpha)$

dove $\alpha$ è uno qualsiasi degli angoli alla circonferenza inscritti nell’arco maggiore $AB$ .

» Teorema delle corde:

$AP\dotPB=CP\dotPD$ , ossia

formula

» Teorema delle secanti:

$PA\dotPB=PD\dotPC$ , ossia

$PA:PD=PC:PB$

» Teorema della tangente e della secante:

$PT^2 = PA\dotPB$ , ossia

$PA : PT=PT : PB$

Altri hanno visualizzato anche

(Questa pagina è stata visualizzata da 264 persone)

Matebook