Circonferenza

-2

 La circonferenza è il luogo geometrico dei punti del piano P(x;y) equidistanti da un punto C(\alpha;\beta) detto centro; tale distanza è il raggio r della circonferenza.

Imponendo d(P;C)=r, ossia \sqrt {(x-\alpha)^2+(y-\beta)^2}=r, ed elevando al quadrato ambo i membri, si ricava l’equazione cartesiana della circonferenza:

(x-\alpha)^2+(y-\beta)^2=r^2.

Sviluppando i quadrati nell’equazione precedente, e ordinando il polinomio, otteniamo:

x^2+y^2-2\alpha x - 2\beta y +\alpha ^2 + \beta ^2 -r^2=0–

Ponendo -2\alpha = a, - 2\beta=b, \alpha ^2 + \beta ^2 -r^2=c, ricaviamo l’equazione:

x^2+y^2+ax+by+c=0,

detta equazione normale o canonica della circonferenza, e si ricavano le relazioni:

  • \alpha= - \frac a 2
  • \beta = -\frac b 2
  • r=\sqrt {(-\frac a 2)^2 + (-\frac b 2)^2-c}=\frac {\sqrt {a^2+b^2-4c}}{2}.

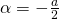
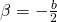
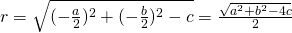Ogni equazione di secondo grado nelle variabili x e y, riconducibile al tipo x^2+y^2+ax+by+c=0 rappresenta una circonferenza di centro C(-\frac a 2; -\frac b 2) e raggio r=\sqrt {(-\frac a 2)^2 + (-\frac b 2)^2-c} se e solo se (-\frac a 2)^2 + (-\frac b 2)^2-c>0, ovvero

a^2+b^2-4c>0 (condizione di realtà del raggio).

Se a^2+b^2-4c=0 la circonferenza degenera nel punto C(-\frac a 2; -\frac b 2).

 La circonferenza di centro O(0;0) e raggio r ha equazione:

x^2+y^2=r^2.

La retta s e la circonferenza \Gamma di centro C e raggio r sono:

  • esterne \leftrightarrow la retta non ha punti in comune con la circonferenza 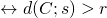\leftrightarrow d(C;s)>r;
  • tangenti 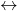\leftrightarrow la retta ha un solo punto (due punti coincidenti) in comune con la circonferenza \leftrightarrow d(C;s)=r;
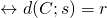  • secanti 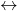\leftrightarrow la retta ha due punti distinti di intersezione con la circonferenza \leftrightarrow d(C;s)<r.

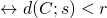E’ possibile anche valutare la posizione di una circonferenza rispetto a una retta osservando che la ricerca delle intersezioni tra una circonferenza e una retta equivale alla ricerca delle soluzioni comuni tra l’equazione della cirocnferenza x^2+y^2+ax+by+c=0 e l’equazione della retta a'x+b'y+c'=0, ovvero alla determinazione delle soluzioni del sistema di secondo grado

\bigg \{\begin{array}{rl} x^2+y^2+ax+by+c=0 \\ a'x+b'y+c'=0 \\ \end{array}

la cui equazione risolvente, ottenuta per sostituzione, risulta un’equazione di secondo grado in una variabile.

Per determinare gli eventuali punti di intersezione tra due circonferenze occorre risolvere il sistema formato dalle loro equazioni:

\bigg \{\begin{array}{rl} x^2+y^2+ax+by+c=0 \\ x^2+y^2+a'x+b'y+c'=0 \\ \end{array}

Se a=a' e b=b', le due circonferenze sono concentriche e quindi non si intersecano; se a\neq a' o b \neq b', applicando il metodo di riduzione, si ottiene l’equazione dell’asse radicale

(a-a')x+(b-b')y+c-c'=0

che rappresenta la retta passante per i punti di intersezione delle due circonferenze, sia nel caso di circonferezne secanti, sia nel caso di circonferenze tangenti, in cui l’asse radicale coincide con la retta tangente comune alle due circonferenze. La retta passante per i centri delle due circonferenze è detta asse centrale e risulta perpendicolare all’asse radicale.

 

Altri hanno visualizzato anche

(Questa pagina è stata visualizzata da 536 persone)

Lascia un commento