Rette tangenti ad una conica

-2

Per determinare le equazioni delle rette tangenti a una conica condotte da un punto P(x_0;y_0) (P esterno caso 1, P appartenente alla conica caso 2) si possono applicare i seguenti procedimenti:.

  • 1° metodo: si scrive l’equazione del fascio proprio 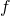f di rette con sostegno nel punto 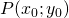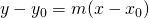P(x_0;y_0), y-y_0=m(x-x_0), si considera il sistema formato dalle equazioni del fascio 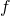f e della conica; ad esempio, per la circonferenza

\bigg \{\begin{array}{rl} y-y_0=m(x-x_0) \\ x^2+y^2+ax+by+c=0 \\ \end{array}

si ricava l’equazione di 2° grado risolvente il sistema e si impone la condizione di tangenza, affinchè le due soluzioni siano coincidenti, ovvero

\Delta = 0.

Se il punto P è esterno, si ottengono due valori distinti di mm che, sostituiti nell’equazione del fascio di rette, consentono di determinare le equazioni delle due rette tangenti (se il punto P ha la stessa ascissa di un estremo del diametro della circonferenza parallelo all’asse x oppure ha la stessa ascissa di un vertice dell’ellisse o dell’iperbole appartenente all’asse x, si ricava un solo valore di m, poichè l’altro tende all’infinito). Nel caso dell’iperbole, se il punto P appartiene ad un suo asintoto, una delle tangenti coincide con l’asintoto stesso, che può quindi essere interpretato come retta tangente all’iperbole in un punto all’infinito.

Se il punto P appartiene alla conica, si ottiene un solo valore di m (due valori coincidenti) che, sostituito nell’equazione del fascio f, consente di determinare l’equazione della retta tangente.

  • 2° metodo: se il punto 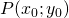P(x_0;y_0) appartiene alla conica si può determinare facilmente l’equazione della retta tangente applicando la formula degli sdoppiamenti:

xx_0 + yy_0+a(\frac {x+x_0}{2})+b(\frac {y+y_0}{2})+c=0 per la circonferenza,

\frac {y+y_0}{2}=axx_0+b\frac {x+x_0}{2}+c [\frac {x+x_0}{2}=ayy_0+b\frac {y+y_0}{2}+c] per la parabola,

\frac {xx_0}{a^2} + \frac {yy_0}{b^2}=1 per l’ellisse,

\frac {xx_0}{a^2} - \frac {yy_0}{b^2}= 1 [\frac {xx_0}{a^2} - \frac {yy_0}{b^2}= -1] per l’iperbole.

  • 3° metodo (solo per la circonferenza): si scrive l’equazione del fascio proprio 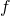f di rette con sostegno nel punto 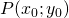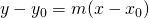P(x_0;y_0), y-y_0=m(x-x_0) e si impone che la distanza tra la generica retta del fascio e il centro 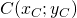C(x_C;y_C) della circonferenza sia uguale al raggio 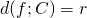d(f;C)=r, ovvero

\frac {|mx_C-y_C-mx_0+y_0|}{\sqrt {mì2+1}}=r.

Si determinano i valori di m e le equazioni delle rette tangenti come nei casi precedenti (se il punto P appartiene alla circonferenza si ricaverà un solo valore di m).

 

Altri hanno visualizzato anche

(Questa pagina è stata visualizzata da 1094 persone)

Lascia un commento