Affinità

-1

Fissato nel piano un sistema di riferimento cartesiano xOy, si definisce affinità una trasformazione geometrica che a ogni punto P(x;y) associa uno ed un solo punto P'(x';y') in modo che valgano le equazioni:

\bigg \{ \begin{array}{rl} x'=ax+by+e \\ y'=cx+dy+f \\ \end{array} ,  con a,b,c,d,e,f \in R
 
 

soddisfacenti la condizione

det A=\begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad-bc \neq 0,

dove

A=\bigg[ \begin{array}{rl} a & b \\ c & d \\ \end{array} \bigg ]

è la matrice dell’affinità.

Le affinità soddisfano le seguenti proprietà:

  • sono trasformazioni invertibili;
  • sono trasformazioni lineari, ovvero trasformano rette in rette;
  • conservano il parallelismo, cioè trasformano rette parallele in rette parallele;
  • a rette incidenti fanno corrispondere rette incidenti;
  • conservano il punto medio di un segmento;
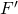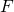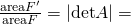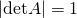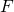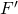  • conservano il rapporto tra le aree corrispondenti, ovvero se F' è la figura trasformata della figura F, attraverso un’affinità, vale \frac {\mathrm{area} F'}{\mathrm {area} F}= |\mathrm{det} A|= rapporto di affinità; se |\mathrm{det}A|=1 si ha affinità equivalente, cioè le figure F e F' sono equivalenti, ovvero hanno la stessa area;
  • se 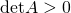\mathrm{det}A >0 l’affinità è detta diretta e conserva il verso di percorrenza;
  • se 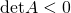\mathrm{det}A<0 l’affinità è detta invertente e non conserva il verso di percorrenza.

 

Altri hanno visualizzato anche:

(Questa pagina è stata visualizzata da 417 persone)

Lascia un commento