Esercizio 21 Problemi sui teoremi di Euclide

Traccia

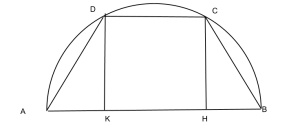
Determinare la misura del perimetro del trapezio isoscele ABCD inscritto in una semicirconferenza di diametro AB, sapendo che la misura della diagonale AC è 24a e che, detta HB la proiezione del lato BC sulla base maggiore AB, è HB=50/13 a. (Posto AB=x, con x>24a, l’equazione risolvente si trova subito applicando il 1° teorema di Euclide al triangolo ABC; si otterrà l’equazione $13x^2-50ax-7488a^2=0$ di cui è accettabile solo una soluzione…)

Svolgimento

Dati

$AC=24a$

$HB=\frac {50}{13}a$

Poniamo $AB=x$ ,

$AH=x-\frac {50}{13}a$

Applicando Euclide abbiamo che

$AH \cdot AB=AC^2$

$(x-\frac {50}{13}a) \cdot x =(24a)^2$

$x^2-\frac {50}{13}ax-576a^2=0$

$13x^2 - 50 ax - 7488 a^2 = 0$

Le cui soluzioni sono:

$x_{\frac 1 2}=\frac{50a \pm \sqrt{2500 + 7488 \cdot 4 \cdot 13}a }{26} =\frac{50a \pm \sqrt{ 391876}a }{26} =\frac{50a \pm 626 a}{26}=\frac {25 \pm 313}{13}$