Esercizio 2 Problema di geometria piana risolubili con l’uso della trigonometria

0

Traccia

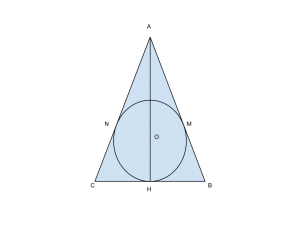
In un triangolo isoscele circoscritto ad un cerchio di raggio r, il rapporto tra l’altezza relativa alla base e la base è \frac {\sqrt 3}{2}. Trovare il perimetro e l’area del triangolo

Svolgeremo questo esercizio con i radianti. Se ci fossero problemi con il loro utilizzo, basta eseguire la seguente sostituzione:

\pi=180^\circ.

 

Svolgimento

triangoloisoscelecircoscritto (1)

 

Prima di tutto, per la risoluzione, occorre ricordare che, chiamando con \mathcal{A} l’area e con p il semiperimetro, vale la seguente formula:

r=\frac {\mathcal{A}}{p}

Chiamiamo con H il punto medio della base BC.

Dalle ipotesi sapremo che:

\frac {AH}{BC}=\frac {\sqrt 3}{2}.

Quindi, sfruttando la metà della base, possiamo dire che:

\frac {AH}{BH}=\sqrt 3.

Denominando con

BH=x,

 

Denominando
BH=x,
avremo:
BC=2x
AH=\sqrt 3 x
AB = \sqrt {AH^2+BH^2}=\sqrt {3x^2+x^2}=\sqrt {4x^2}=2 x
quindi il triangolo è equilatero..
Calcoliamo l’area:
\frac 12 BC \cdot AH = \frac 12 2 x * x \sqrt3 = \sqrt 3 x^2.
Calcoliamo il perimetro:
3 \cdot BC = 6 x.
Riscriviamo la relazione tra il raggio del cerchio INSCRITTO…
r = \frac {\mathcal{A}}{p}.
r = \frac {\sqrt 3 x^2}{3x}= \frac {x}{\sqrt 3}
da questo adesso finalmente ricaviamo:
x = r \sqrt 3
e da x ricaviamo tutti i lati del triangolo:
BC = AB = AC = 2r \sqrt 3
2p = 6r \sqrt 3

(Questa pagina è stata visualizzata da 223 persone)

Lascia un commento