Esercizio 5 Problema di geometria piana risolubili con l'uso della trigonometria

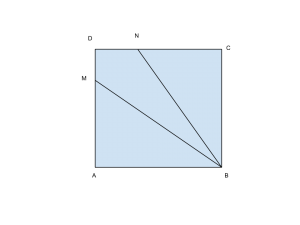
Traccia

In un quadrato ABCD si consideri sul lato AD il punto M tale che 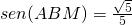$sen (ABM) = \frac {\sqrt 5}{5}$ e sul lato CD il punto N tale che 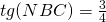$tg (NBC) = \frac 34$ . Sapendo che il lato del quadrato ha per misura 8, si trovino:

la misura del perimetro e l’area del triangolo MBN
il 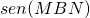$sen (MBN)$ dopo aver verificato che il triangolo MBN è rettangolo
la misura del raggio della circonferenza circoscritta a MBN

Svolgeremo questo esercizio con i radianti. Se ci fossero problemi con il loro utilizzo, basta eseguire la seguente sostituzione:

$\pi=180^\circ$ .

Svolgimento

Dai dati abbiamo giusto qualche informazione che possiamo ampliare trovando tutte le varie funzioni trigonometriche oltre a quelle forniteci.

Sappiamo che:

$sen (ABM) =\frac {\sqrt {5}}{5}$ ,

quindi, considerando di prendere in considerazione solo il risultato positivo del coseno, e sfruttando l’uguaglianza

$sen^2(\alpha)+cos^2(\alpha)=1$ , avremo

$cos (ABM)=\sqrt {1-sen^2 (ABM)}=\sqrt{1-\frac {1}{5}}=\sqrt {\frac 45}=\frac {2}{\sqrt 5}=\frac {2\sqrt 5}{5}$

$tg(ABM)=\frac {sen(ABM)}{cos(ABM)}=\frac 12$ .

Allo stesso modo, avremo:

$tg(NBC)=\frac 34$

$sen(NBC)=\frac 34 cos (NBC)$

Riportando tutto sulla relazione fondamentale avremo:

$sen^2(NBC)+cos^2(NBC)=1$

$\frac {9}{16} cos^2(NBC)+cos^2(NBC)=1$

$\frac {25}{16}cos^2(NBC)=1$

$cos^2(NBC)=\frac {16}{25}$

$cos(NBC)=\frac 45$

e così:

$sen(NBC)=\frac 35$

Dal grafico ora posiamo iniziare ad ottenere:

$AB=MB \cdot cos (ABM)$

$MB=\frac {AB}{cos(ABM)}=4 \sqrt 5$

Allo stesso modo:

$NB=\frac {CB}{cos(NBC)}=10$

Osservando la figura notiamo come:

$\widehat{NBC}+ \widehat{NBM}+\widehat{ABM}=90^\circ$

Così avremo che:

$\widehat{NBM}=90-\widehat{NBC}- \widehat{ABM}$

e, sapendo che:

$cos (90-\alpha)=sen(\alpha)$ , avremo:

$cos(\widehat{NBM}=cos(90-\widehat{NBC}- \widehat{ABM})$

da cui:

$cos(\widehat{NBM}=sen(\widehat{NBC}+ \widehat{ABM})$ .

Ricordando che:

$sen(\alpha+\beta)=sen(\alpha)cos(\beta)+sen(\beta)cos(\alpha)$ , otteniamo:

$cos(\widehat{NBM})=\frac 35 \cdot \frac {2\sqrt 5}{5} + \frac 45 \cdot \frac {\sqrt 5}{5}=\frac {6\sqrt 5}{25}+\frac {4\sqrt 5}{25}=\frac {10\sqrt5}{25}=\frac {2\sqrt 5}{5}$ .