Esercizio 11 Problemi di geometria

Traccia

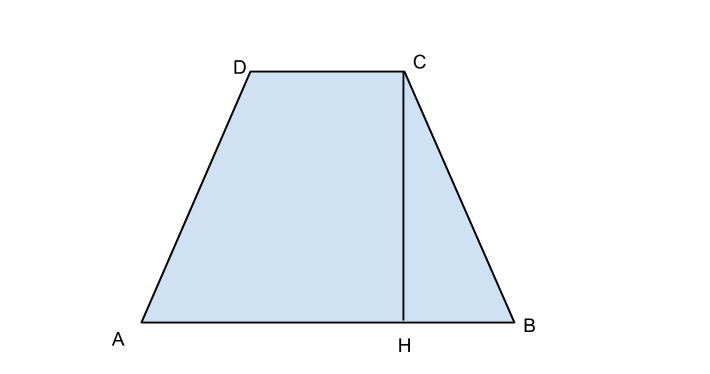
In un trapezio isoscele la base minore è i $\frac 25$ del lato obliquo, il perimetro è 80 cm e la somma della quarta parte della base maggiore con la metà della base minore è 12 cm. Verificare che il trapezio è circoscrivibile a una circonferenza e calcolarne il diametro.

Svolgimento

Dai dati avremo:

$CD=\frac 25 BC$

$2p=80 \mbox { cm}$

$\frac 14 AB + \frac 12 CD=12 \mbox { cm}$

Ponendo $BC=x$ , otteniamo:

$CD=\frac 25x$

e sostituendo nell’altra:

$\frac 14 AB+ \frac 12 \frac 25x =12$

$\frac 14 AB+ \frac 15x =12$

$5AB=240-4x$

$AB=48 - \frac 45 x$

Inserendo tutto nell’equazione del perimetro ricaviamo l’incognita:

$48 - \frac 45 x+x+\frac 25 x +x =80$

$2x- \frac 25 x =32$

$\frac 85 x =32$

$x=20$

Ricaviamo i lati:

$AB=32 \mbox { cm}$

$BC=AD=20 \mbox { cm}$

$CD= 8 \mbox { cm}$

Affinchè il trapezio sia circoscrivibile deve essere uguale la somma dei lati opposti, e quindi:

$AB+CD=AD+BC$ , che è verificato.

Calcoliamo quindi il diametro, che equivale all’altezza del trapezio, sfruttando il triangolo rettangolo BHC e che

$BH=\frac 12 (AB-CD)=12 \mbox { cm}$ :

$CH=\sqrt { BC^2-BH^2}=\sqrt { 20^2 - 12^2 }\mbox { cm}=\sqrt { 400 - 144 }\mbox { cm}=\sqrt { 256 }\mbox { cm}=16\mbox { cm}$ .

Altri esercizi simili:

(Questa pagina è stata visualizzata da 64 persone)

Lascia un commento Annulla risposta