Esercizio 12 Problemi di geometria

Traccia

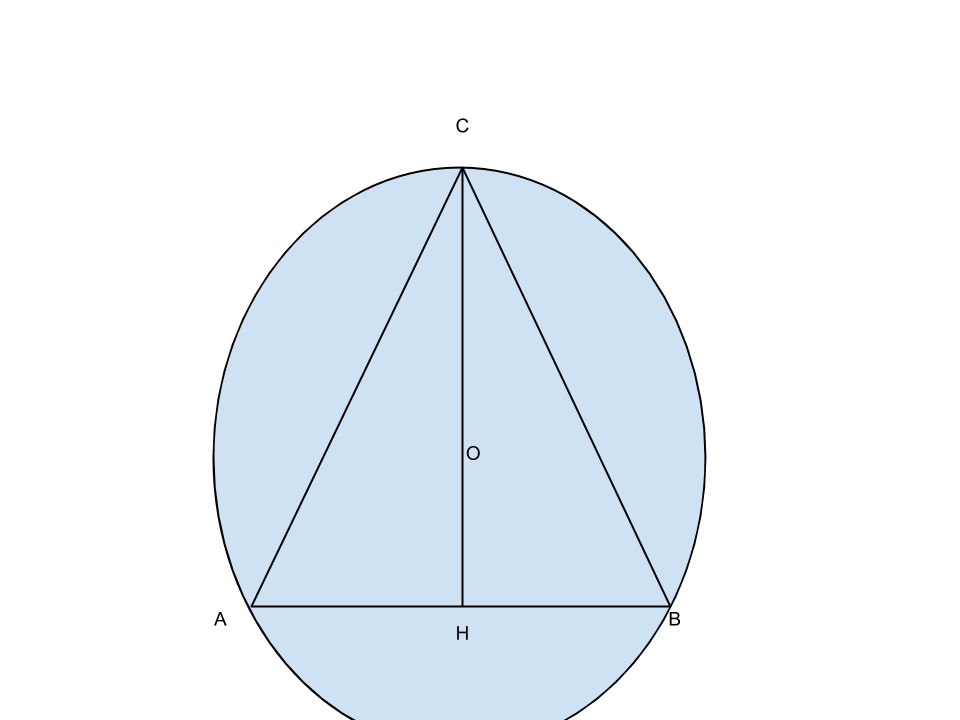
Un triangolo isoscele $ABC$ , di base $AB$ e altezza $CH$ , è inscritto in una circonferenza di centro $O$ . Sapendo che

$\frac 29 CH + \frac 16 AB=CH-AB=3 \mbox{ cm }$

, si verifichi che la distanza tra $O$ e i lati congruenti è $\sqrt{\frac 52}$ cm.

Svolgimento

Ponendo $AB=x$ , dai dati avremo:

$CH=x+3$

$4CH + 3x = 54$ .

Sostituendo otteniamo:

$4x+12+3x=54$

$7x=42$

$x=6$

da cui:

$AB=6 \mbox { cm}$

$CH=9 \mbox { cm}$ .

Per calcolare la distanza tra il segmento ci serve calcolare il lato obliquo del triangolo perche la formula del raggio è:

$r=\frac {AB \cdot BC \cdot AC}{4A}=\frac {AB \cdot BC \cdot AC}{4\frac {AB \cdot CH}{2}}=\frac {BC \cdot AC}{2CH}$

quindi:

$AC=AB=\sqrt {CH^2+AH^2}=\sqrt {9^2+3^2}\mbox { cm}=\sqrt {81+9}\mbox { cm}=\sqrt {90}\mbox { cm}=3\sqrt {10}\mbox { cm}$ .

quindi:

$r=\frac {3 \sqrt {10} \cdot 3 \sqrt {10}}{18}\mbox { cm}=5\mbox { cm}$

Ora, per trovare la distanza, basterà considerare i due triangoli ACH e OCK, e vedere che questi sono simili, di conseguenza:

$OK:AH=OC:AC$

$OK=\frac {AH \cdot OC}{AC}=\frac {3 \cdot 5 }{3 \sqrt {10}}\mbox { cm}=\frac {5}{\sqrt {10}}\mbox { cm}=\sqrt {\frac 52}\mbox { cm}$ . cvd

Altri esercizi simili:

(Questa pagina è stata visualizzata da 69 persone)

Matebook