Esercizio 15 Problemi di geometria

Traccia

In un triangolo rettangolo la somma dei $\frac 23$ del cateto minore e dei $\frac 38$ del maggiore è 21 cm e la differenza delle lunghezze dei cateti è 6 cm. determinare la lunghezza del raggio della circonferenza inscritta dopo aver dimostrato che la somma dei cateti supera l’ipotenusa di un segmento avente la lunghezza del diametro della circonferenza inscritta.

Svolgimento

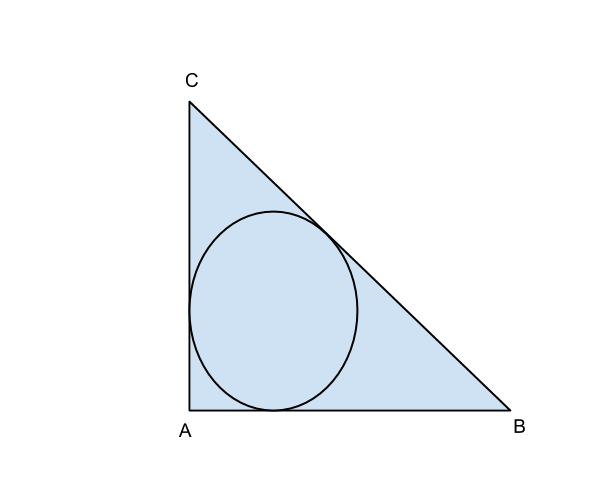
Supponiamo che l’ipotenusa del triangolo sia BC, dai dati otteniamo:

$\frac 23 AC+ \frac 38 AB=21$

$AB-AC=6$

Ponendo $AC=x$ , otteniamo:

$AB=x+6$

$\frac 23 x + \frac 38 (x+6)=21$

$16x+9x+54=504$

$25x=450$

$x=18$

Da cui:

$AC=18 \mbox { cm}$

$AB= 24 \mbox { cm}$

Calcoliamo l’ipotenusa con Pitagora:

$BC=\sqrt {AB^2+AC^2}=\sqrt {24^2+18^2}\mbox { cm}=\sqrt {576+324}\mbox { cm}=\sqrt {900}\mbox { cm}=30\mbox { cm}$ .

Il raggio della circonferenza inscritta è:

$r=\frac {A}{p}$

Ora, calcoliamo l’area e il semiperimetro:

$A_{ABC}=\frac {AB\cdot AC}{2}=\frac {24 \cdot 18}{2}\mbox { cm}^2=216 \mbox { cm}^2$

$2p=(18+24+30)\mbox { cm}=72 \mbox { cm}$

Quindi il raggio sarà:

$r=\frac {216}{36}\mbox { cm}=6\mbox { cm}$ .

Altri esercizi simili:

(Questa pagina è stata visualizzata da 59 persone)

Lascia un commento Annulla risposta

Devi essere connesso per inviare un commento.