Esercizio 21 Problemi di geometria

0

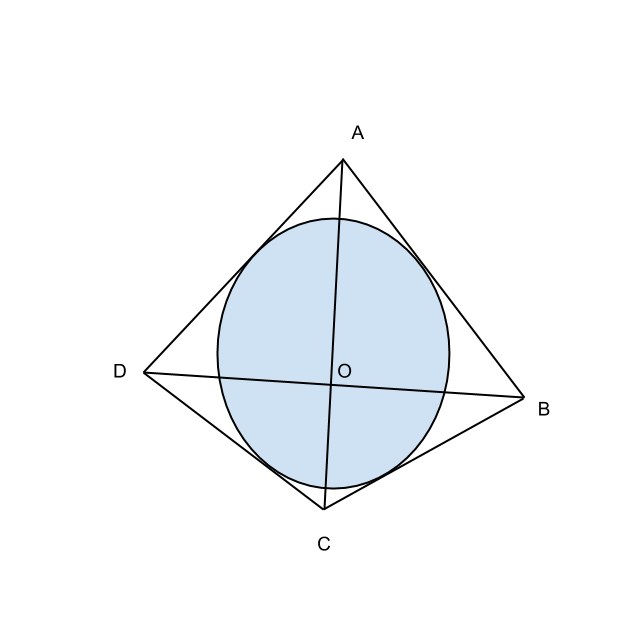
Traccia

Le diagonali del quadrilatero ABCD sono perpendicolari e si incontrano in O punto medio della diagonale BD. Determinare i lati del quadrilatero sapendo che il suo perimetro è di 84 cm e che

    \[\frac 12 DC+\frac 23 AD=24 \mbox { cm }\]

Dimostrare poi che il quadrilatero è circoscrivibile a una circonferenza e, sapendo che gli angoli \widehat{ABC} e \widehat{ADC} sono retti, calcolare il raggio della circonferenza inscritta.

Svolgimento

quadrilatero con circonferenza (1)

Dalla traccia ricaviamo che:

2p=84 \mbox { cm},

ma che, essendo questo un romboide, i lati sono a due a due congruenti, e quindi:

2AD+2DC=84 \mbox { cm} \Rightarrow AD+DC=42\mbox { cm}.

Ponendo AD=x e DC=y otteniamo:

\begin{cases} x+y=42 \\ \frac 12 y + \frac 23 x =24 \end {cases}

\begin{cases} x+y=42 \\ \3 y + 4 x =144 \end {cases}

\begin{cases} x=42-y \\ \3 y + 4(42-y) =144 \end {cases}

\begin{cases} x=42-y \\ \3 y -4y+ 168=144 \end {cases}

\begin{cases} x=42-y \\ \y=24 \end {cases}

\begin{cases} x=18 \\ \y=24 \end {cases}

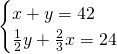
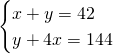
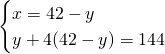
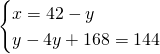
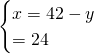
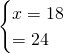
Avremo quindi:

AD=AB=18 \mbox { cm}

DC=CB=24 \mbox { cm}.

Affinchè sia circoscrivibile, le somme delle misure dei lati opposti devono essere uguali, e quindi, si verifica facilmente che:

AD+CB=AB+CD…

Per trovare il raggio sarà necessario trovare l’area. Calcoliamo la diagonale AC con il teorema di Pitagora:

AC =\sqrt {BC^2 +AB^2}=\sqrt {24^2+18^2}\mbox { cm}=\sqrt {576+324}\mbox { cm}=\sqrt {900}\mbox { cm} = 30\mbox { cm}

Ricaviamo BO, metà di BD, uguagliando l’area del triangolo rettangolo ABC:

A_{ABC}=\frac {AB \cdot BC}{2}=\frac {AC \cdot BO}{2}

Quindi avremo:

BO=\frac {AB \cdot BC}{AC}=\frac {18\cdot 24}{30}\mbox { cm}=\frac {72}{5}\mbox { cm}

BD=\frac {144}{5}\mbox { cm}

L’area del quadrilatero sarà quindi:

A_{ABCD}=\frac {AC \cdot BD}{2}=\frac {30 \cdot \frac {144}{5}}{2}\mbox { cm}^2=432\mbox { cm}^2

e infine possiamo calcolare il raggio

r=\frac {A}{ p} = \frac {432}{42}\mbox { cm}=\frac {72}{7}\mbox { cm}

Volendo il raggio lo si poteva calcolare come altezza di uno dei triangolini \cdots)
 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 70 persone)

Lascia un commento