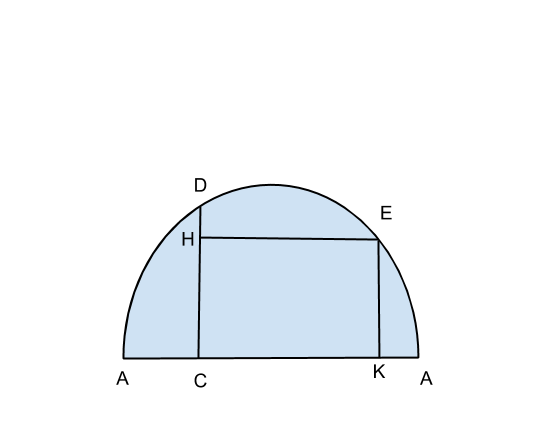
Traccia
E’ data una semicirconferenza di diametro ![]() 12 cm; il punto
12 cm; il punto ![]() divide
divide ![]() in parti proporzionali ai numeri 1 e 4. Si conduca da
in parti proporzionali ai numeri 1 e 4. Si conduca da ![]() la perpendicolare ad
la perpendicolare ad ![]() che incontri in
che incontri in ![]() la semicirconferenza e, dopo aver determinato
la semicirconferenza e, dopo aver determinato ![]() , si determini sull’arco
, si determini sull’arco ![]() un punto
un punto ![]() in modo che si abbia
in modo che si abbia
![]()
, essendo ![]() e
e ![]() le proiezioni ortogonali di
le proiezioni ortogonali di ![]() rispettivamente su
rispettivamente su ![]() e
e ![]() . Come risulta il quadrilatero
. Come risulta il quadrilatero ![]() ?
?
Svolgimento
Dai dati abbiamo che:
![]()
![]()
Sappiamo anche che:
![]()
o meglio
![]() .
.
Sostituendo sopra otteniamo:
![]()
![]()
![]() .
.
Per ricavare CD, sfruttiamo il fatto che il triangolo ADB sia inscritto in una semicirconferenza e di conseguenza rettangolo. Con il secondo teorema di Euclide avremo:
![]() .
.
Risolviamo ora la seconda parte, ponendo ![]() , e
, e ![]() , così da avere:
, così da avere:
![]() .
.
![]()
![]()
Quindi, con le due condizioni dateci dalla traccia, risolviamo il sistema:
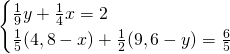
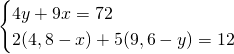
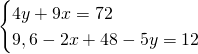
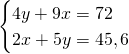
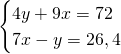
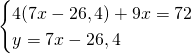
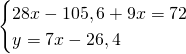
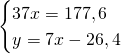
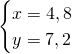
Ma essendo questi due valori esattamente congruenti ai valori trovati precedentemente, otteniamo che:
![]() .
.
Quindi il quadrilatero risulta essere proprio un rettangolo…
Altri esercizi simili:
- Esercizio 1 Problema di geometria
- Esercizio 2 Problema di geometria
- Esercizio 3 Problema di geometria
- Esercizio 4 Problema di geometria
- Esercizio 5 Problema di geometria
- Esercizio 6 Problemi di geometria
- Esercizio 7 Problemi di geometria
- Esercizio 8 Problemi di geometria
- Esercizio 9 Problemi di geometria
- Esercizio 10 Problemi di geometria
- Esercizio 11 Problemi di geometria
- Esercizio 12 Problemi di geometria
- Esercizio 13 Problemi di geometria
- Esercizio 14 Problemi di geometria
- Esercizio 15 Problemi di geometria
- Esercizio 16 Problemi di geometria
- Esercizio 17 Problemi di geometria
- Esercizio 18 Problemi di geometria
- Esercizio 19 Problemi di geometria
- Esercizio 20 Problemi di geometria
- Esercizio 21 Problemi di geometria
- Esercizio 22 Problemi di geometria
- Esercizio 23 Problemi di geometria
- Esercizio 24 Problemi di geometria
- Esercizio 25 Problemi di geometria
- Esercizio 26 Problemi di geometria
(Questa pagina è stata visualizzata da 82 persone)