Esercizio 3 Problema di geometria

Traccia

In una circonferenza di diamtro $AB=$ 30 cm è data una corda $CD$ perpendicolare nel punto $M$ al diametro $AB$ . Sapendo che

$\frac 34 AM + \frac 13 MB=20 cm$

, determinare l’area del quadrilatero $ABCD$ . (Porre $AM=x$ ).

Svolgimento

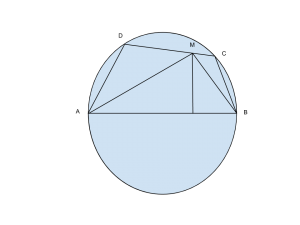
Dal disegno si evince subito che i triangoli ABC e ABD sono retti, e che M risulterà essere il punto medio della corda CD.

Ponendo $AM=x$ , otteniamo:

$MB=30-x$ , e quindi:

$\frac 34 x + \frac 13 (30-x) =20$

$\frac 34x + 10-\frac 13 x =20$

$\frac {9-4}{12}x=10$

$\frac {5}{12}x=10$

$x=24$

Quindi:

$AM=24 \mbox { cm}$

$BM=6 \mbox { cm}$

Ricaviamo CM con il secondo teorema di Euclide:

$CM=\sqrt {AM \cdot MB}=\sqrt {24 \cdot 6} \mbox { cm}=12 \mbox { cm}$

Così l’area del quadrilatero ABCD sarà il doppio dell’area del triangolo rettangolo, di cui sappiamo l’ipotenusa e la sua altezza relativa:

$A_{ABCD}=2A_{ABC}=2 \frac {AB \cdot CM}{2}=AB \cdot CM=(30 \cdot 12) \mbox { cm}^2=360\mbox { cm}^2$ .

Altri esercizi simili:

(Questa pagina è stata visualizzata da 270 persone)

Matebook