Esercizio 4 Problema di geometria

Traccia

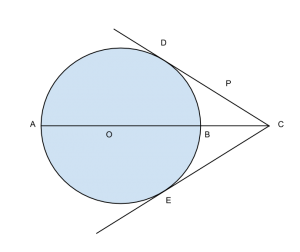
E’ data una circonferenza di centro $O$ e di diametro $AB=6a$ ; si prolunghi il diametro $AB$ , oltre $B$ , di un segmento $BC=2a$ e da $C$ si conducano le due tangenti alla circonferenza. Detti $D$ ed $E$ i due punti di contatto, si determini il segmento $CP=x$ , su $CD$ , in modo che sia verificata la seguente relazione:

$\frac 34 CE - 2PC = \frac 13 PD$

. Determinare, poi, il perimetro e l’area del quadrilatero $ODCE$ .

Svolgimento

Dai dati e dal grafico si evince subito che:

$OB=3a$

$OC=5a$

Sappiamo anche che OD equivale al raggio, 3a, e che questo sarà perpendicolare al segmento di tangenza. Di conseguenza, possiamo ricavare subito il lato DC con il teorema di Pitagora sul triangolo ODC:

$DC=\sqrt {OC^2-DO^2}=\sqrt {25-9}a=\sqrt {16}a=4a$ .

Ponendo $PC=x$ da traccia, otteniamo:

$PD=4a-x$ .

Analizziamo ora la relazione sapendo che i segmenti di tangenza sono congruenti per definizione:

$\frac 34 4a -2x=\frac 13 (4a-x)$

$3a-2x=\frac 43 a - \frac 13 x$

$9a-6x=4a-x$

$5x=5a$

$x=a$

Quindi ora ricaviamo perimetro e area del quadrilatero:

$2p_{ODCE}=3a+4a+4a+3a=14a$

$A_{ODCE}=2A_{ODC}=2 \frac {OD \cdot DC}{2}=3a \cdot 4a= 12a^2$ .

Altri esercizi simili:

(Questa pagina è stata visualizzata da 128 persone)

Lascia un commento Annulla risposta

Devi essere connesso per inviare un commento.