- Relazioni fondamentali della goniometria
Tra le funzioni goniometriche esistono relazioni fondamentali.
La prima: la somma dei quadrati del seno e del coseno di uno stesso arco vale 1:
![]() .
.
La seconda: la tangente di un arco vale il rapporto tra il seno e il coseno dell’arco:
![]() .
.
- Legami tra le funzioni goniometriche
| noto | |||
| |
|||
| |
|||
| |
- Valori delle funzioni circolari di archi o di angoli notevoli
| gradi | ||||||||
| radianti | ||||||||
| |
|
|||||||
| |
|
|
||||||
| |
|
|
- Relazioni particolari tra coppie di angoli che differiscono per multipli di angolo retto
| angolo | seno | coseno | tangente | cotangente |
- Formule di sottrazione e di addizione
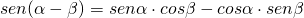
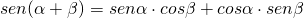
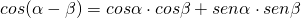
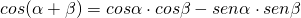
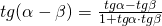 , con
, con 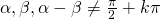
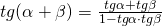 , con
, con 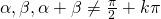
- Formule di duplicazione
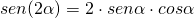
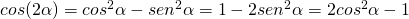
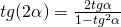 con
con 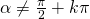 e
e 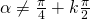
- Formule parametriche
-
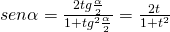 con
con 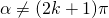
-
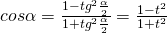 con
con 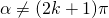
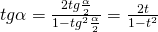 con
con 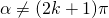 e
e 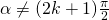
- Formule di bisezione
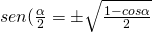
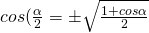
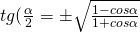 con
con 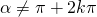
- Formule di prostaferesi
- Formule di Werner
(Questa pagina è stata visualizzata da 247 persone)